5. Vectors

b. Vector Addition

3. Properties

We here list the algebraic properties of vector addition and its relation to magnitude.

In the following, u⃗\vec u, v⃗\vec v, and w⃗\vec w are vectors. Also, 0⃗=⟨0,0⟩\vec 0=\langle0,0\rangle is called the Zero Vector which is the vector whose components are both zero , while −v⃗=⟨−v1,−v2⟩-\vec v=\langle-v_1,-v_2\rangleis called the Negative of v⃗\vec v which is the vector whose components are the negatives of those for v⃗\vec v.

First, there are 77 properties involving just vector addition.

Vector Addition Properties
Let u⃗\vec u, v⃗\vec v, and w⃗\vec w be arbitrary vectors. Then,

  1. Addition is Commutative:   u⃗+v⃗=v⃗+u⃗\vec u+\vec v=\vec v+\vec u  

Proof

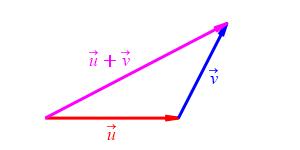
u⃗+v⃗=⟨u1,u2⟩+⟨v1,v2⟩=⟨u1+v1,u2+v2⟩=⟨v1+u1,v2+u2⟩=⟨v1,v2⟩+⟨u1,u2⟩=v⃗+u⃗\begin{aligned} \vec u+\vec v &=\left\langle u_1,u_2\right\rangle+\left\langle v_1,v_2\right\rangle =\left\langle u_1+v_1,u_2+v_2\right\rangle \\ &=\left\langle v_1+u_1,v_2+u_2\right\rangle =\left\langle v_1,v_2\right\rangle+\left\langle u_1,u_2\right\rangle \\ &=\vec v+\vec u \end{aligned} A geometrical proof was also given on the previous page.

[×]
  1. Addition is Associative:   (u⃗+v⃗)+w⃗=u⃗+(v⃗+w⃗)(\vec u+\vec v)+\vec w=\vec u+(\vec v+\vec w)  

Proof

(u⃗+v⃗)+w⃗=(⟨u1,u2⟩+⟨v1,v2⟩)+⟨w1,w2⟩=⟨u1+v1,u2+v2⟩+⟨w1,w2⟩=⟨u1+v1+w1,u2+v2+w2⟩=⟨u1,u2⟩+⟨v1+w1,v2+w2⟩=⟨u1,u2⟩+(⟨v1,v2⟩+⟨w1,w2⟩)=u⃗+(v⃗+w⃗)\begin{aligned} (\vec u+\vec v)+\vec w &=\big(\left\langle u_1,u_2\right\rangle+\left\langle v_1,v_2\right\rangle\big) +\left\langle w_1,w_2\right\rangle \\ &=\left\langle u_1+v_1,u_2+v_2\right\rangle+\left\langle w_1,w_2\right\rangle \\ &=\left\langle u_1+v_1+w_1,u_2+v_2+w_2\right\rangle \\ &=\left\langle u_1,u_2\right\rangle+\left\langle v_1+w_1,v_2+w_2\right\rangle \\ &=\left\langle u_1,u_2\right\rangle +\big(\left\langle v_1,v_2\right\rangle+\left\langle w_1,w_2\right\rangle\big) \\ &=\vec u+(\vec v+\vec w) \end{aligned}

[×]
  1. 0⃗\displaystyle \vec 0 is the Zero or Additive Identity:   v⃗+0⃗=v⃗\displaystyle \vec v+\vec 0=\vec v  

Proof

v⃗+0⃗=⟨v1,v2⟩+⟨0,0⟩=⟨v1+0,v2+0⟩=⟨v1,v2⟩=v⃗\begin{aligned} \vec v+\vec 0 &=\left\langle v_1,v_2\right\rangle+\left\langle0,0\right\rangle \\ &=\left\langle v_1+0,v_2+0\right\rangle \\ &=\left\langle v_1,v_2\right\rangle \\ &=\vec v \end{aligned}

[×]
  1. −v⃗-\vec v is the Negative or Additive Inverse of v⃗\vec v:   v⃗+(−v⃗)=0⃗\displaystyle \vec v+(-\vec v)=\vec 0  

Proof

v⃗+(−v⃗)=⟨v1,v2⟩+⟨−v1,−v2⟩=⟨v1−v1,v2−v2⟩=⟨0,0⟩=0⃗\begin{aligned} \vec v+(-\vec v) &=\left\langle v_1,v_2\right\rangle+\left\langle-v_1,-v_2\right\rangle \\ &=\left\langle v_1-v_1,v_2-v_2\right\rangle \\ &=\left\langle0,0\right\rangle=\vec 0 \end{aligned}

[×]
  1. The Zero Vector, 0⃗\vec 0, is Unique:
       If z⃗\vec z is a vector which satisfies v⃗+z⃗=v⃗\vec v+\vec z=\vec v, then z⃗=0⃗\vec z=\vec 0.  

Proof

If z⃗=⟨z1,z2⟩\vec z=\left\langle z_1,z_2\right\rangle and v⃗=⟨v1,v2⟩\vec v=\left\langle v_1,v_2\right\rangle, then: v⃗+z⃗=⟨v1+z1,v2+z2⟩ \vec v+\vec z=\left\langle v_1+z_1,v_2+z_2\right\rangle So the equation v⃗+z⃗=v⃗\vec v+\vec z=\vec v says: v1+z1=v1andv2+z2=v2 v_1+z_1=v_1 \qquad \text{and} \qquad v_2+z_2=v_2 So z1=0z_1=0 and z2=0z_2=0, or z⃗=0⃗\vec z=\vec 0.

[×]
  1. The Negative, −v⃗-\vec v, is Unique:
       Given a vector v⃗\vec v, if a vector w⃗\vec w satisfies v⃗+w⃗=0⃗\vec v+\vec w=\vec 0, then w⃗=−v⃗\vec w=-\vec v.  

Proof

If w⃗=⟨w1,w2⟩\vec w=\left\langle w_1,w_2\right\rangle and v⃗=⟨v1,v2⟩\vec v=\left\langle v_1,v_2\right\rangle, then: v⃗+w⃗=⟨v1+w1,v2+w2⟩ \vec v+\vec w=\left\langle v_1+w_1,v_2+w_2\right\rangle So the equation v⃗+w⃗=0⃗\vec v+\vec w=\vec 0 says: v1+w1=0andv2+w2=0 v_1+w_1=0 \qquad \text{and} \qquad v_2+w_2=0 So w1=−v1w_1=-v_1 and w2=−v2w_2=-v_2, or w⃗=−v⃗\vec w=-\vec v.

[×]
  1. Additive Cancellation:
       If u⃗+v⃗=w⃗+v⃗\vec u+\vec v=\vec w+\vec v, then u⃗=w⃗\vec u=\vec w.  

Proof

If u⃗=⟨u1,u2⟩\vec u=\left\langle u_1,u_2\right\rangle, v⃗=⟨v1,v2⟩\vec v=\left\langle v_1,v_2\right\rangle and w⃗=⟨w1,w2⟩\vec w=\left\langle w_1,w_2\right\rangle, then: u⃗+v⃗=⟨u1+v1,u2+v2⟩ \vec u+\vec v=\left\langle u_1+v_1,u_2+v_2\right\rangle and w⃗+v⃗=⟨w1+v1,w2+v2⟩ \vec w+\vec v=\left\langle w_1+v_1,w_2+v_2\right\rangle So the equation u⃗+v⃗=w⃗+v⃗\vec u+\vec v=\vec w+\vec v says: u1+v1=w1+v1andu2+v2=w2+v2 u_1+v_1=w_1+v_1 \qquad \text{and} \qquad u_2+v_2=w_2+v_2 So u1=w1u_1=w_1 and u2=w2u_2=w_2, or u⃗=w⃗\vec u=\vec w.

[×]

Further, vector addition is related to magnitude by the triangle inequality which basically says that each side of a triangle is shorter than the sum of the other two sides and longer than the difference between the other two sides:

Triangle Inequality
Let u⃗\vec u and v⃗\vec v be arbitrary vectors. Then,

  1. Triangle Inequality:   ∣∣u⃗∣−∣v⃗∣∣≤∣u⃗+v⃗∣≤∣u⃗∣+∣v⃗∣\left|\rule{0pt}{9pt}\,|\vec u|-|\vec v|\,\right| \le |\vec u+\vec v| \le |\vec u|+|\vec v|

⟸⟸\quad\Longleftarrow\quad\Longleftarrow\quad Read this. It's easy and informative!

pf_TriIneq5

Optional
Vector Addition Properties 5, 6 and 7 were proved above by writing out the components of the equations. They can also be proved using only Vector Addition Properties 1-4, without writing out any components. These proofs will be assigned in the exercises.

© 2025 MYMathApps

Supported in part by NSF Grant #1123255